NumPy和Matplotlib快速入门教案¶
课程概述¶
本教案通过正弦波的生成和绘制,帮助初学者快速掌握NumPy数组操作和Matplotlib基本绘图。课程采用"理论+实践"的模式,每个概念都配有相应的代码示例和练习。
课程时长:45分钟
难度级别:初级
前置知识:Python基础语法
教学目标¶
通过本课程的学习,你将能够:
NumPy核心技能:
创建数组:
np.array(),np.arange(),np.linspace()数学运算:
np.sin(),np.cos(), 向量化操作复数操作:实部
.real,虚部.imag
Matplotlib核心技能:
基本绘图:
plt.plot()多子图:
plt.subplot()图表美化:标题、坐标轴、网格、图例
实际应用:
生成正弦波信号
可视化信号波形
比较不同参数的信号
学习建议:
跟着代码示例动手实践
完成所有练习和思考问题
尝试修改参数观察效果
记录学习过程中的疑问和发现
第1部分:NumPy基础 (15分钟)¶
1. NumPy数组创建和操作¶
import numpy as np
# 创建数组的多种方式
arr1 = np.array([1, 2, 3, 4, 5]) # 从列表创建
arr2 = np.arange(0, 10, 0.5) # 类似range,但支持小数步长
arr3 = np.linspace(0, 2*np.pi, 100) # 等间隔数列,0到2π之间100个点
print("arange:", arr2[:5]) # 前5个元素
print("linspace:", arr3[:5])
关键概念:
np.arange(start, stop, step)- 创建等差序列np.linspace(start, stop, num)- 创建指定数量的等间隔点
[problem 1]:arange和linspace比较
# 使用arange创建时间序列
duration = 0.01 # 0.01秒
sample_rate = 32000 # 32kHz采样频率
t_arange = np.arange(0, duration, 1/sample_rate)
# 使用linspace创建相同的时间序列
num_points = int(sample_rate * duration)
t_linspace = np.linspace(0, duration, num_points, endpoint=...) // 1: Ture 或 False ?
print(f"arange创建的点数: {len(t_arange)}")
print(f"linspace创建的点数: {len(t_linspace)}")
print(f"时间点是否相同: {np.allclose(t_arange, t_linspace)}")
# 比较两种方法的差异
print(f"arange最后一个时间点: {t_arange[-1]:.6f}")
print(f"linspace最后一个时间点: {t_linspace[-1]:.6f}")
思考问题:
为什么两种方法创建的时间序列不完全相同?
在实际应用中,哪种方法更适合创建固定时间间隔的序列?
当需要精确控制采样点数时,应该使用哪种方法?
2. NumPy数学运算¶
# 基本数学运算 - 向量化操作(无需循环!)
t = np.linspace(0, 2*np.pi, 100)
sin_wave = np.sin(t) # 对数组中每个元素求正弦
cos_wave = np.cos(t) # 对数组中每个元素求余弦
# 数组运算
amplitude = 2
frequency = 1
phase = np.pi/4
# 正弦波公式: A * sin(2πft + φ)
wave = amplitude * np.sin(2 * np.pi * frequency * t + phase)
关键概念:
向量化运算:对整个数组进行数学运算,无需循环
NumPy函数自动应用于数组的每个元素
[problem 2]:正弦余弦平方和验证
# 生成时间序列
duration = 0.01 # 0.01秒
sample_rate = 32000 # 32kHz采样频率
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)
# 生成正弦和余弦信号
freq = 1000 # 1kHz频率
amplitude = 1
sin_wave = amplitude * np.sin(2 * np.pi * freq * t)
cos_wave = amplitude * np... // 1
# 验证平方和是否为常数
square_sum = sin_wave**2 + ... // 2
print(f"平方和的最小值: {np.min(square_sum):.6f}")
print(f"平方和的最大值: {np.max(square_sum):.6f}")
print(f"平方和是否为常数: {np.allclose(square_sum, 1)}")
# 验证不正交的情况(不同频率)
sin_wave2 = amplitude * np.sin(2 * np.pi * 500 * t) # 500Hz
cos_wave2 = amplitude * np.cos(2 * np.pi * ... * t) # 1000Hz // 3
square_sum2 = sin_wave2**2 + cos_wave2**2
print(f"不同频率的平方和是否为常数: {np.allclose(square_sum2, 1)}")
print(f"平方和的最小值: ...") // 4
print(f"平方和的最大值: ...") // 5
思考问题:
为什么相同频率的正弦和余弦信号的平方和是常数?
不同频率的正弦和余弦信号为什么平方和不是常数?
这个性质在信号处理中有什么应用?
3. 复数支持¶
关键概念:
# 复数在信号处理中很重要
real_part = np.array([1, 2, 3])
imag_part = np.array([4, 5, 6])
complex_signal = real_part + 1j * imag_part # 创建复数数组
print("复数数组:", complex_signal)
print("实部:", complex_signal.real)
print("虚部:", complex_signal.imag)
问题:
虚部是否含有虚数符号 i 或 j?
如何由 complex_signal.real 和 complex_signal.imag 合成一个复数数组?
[problem 3]:复数信号操作
# 生成时间序列
duration = 0.01 # 0.01秒
sample_rate = 32000 # 32kHz采样频率
t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)
# 创建复数信号(欧拉公式:e^(jωt) = cos(ωt) + j*sin(ωt))
freq = 1000 # 1kHz频率
complex_signal = np.exp(1j * 2 * np.pi * freq * t)
# 方法1:使用abs函数计算模
magnitude1 = np //1
# 方法2:使用实部和虚部计算模
magnitude2 = np.sqrt(...) //2
print(f"两种方法计算的模是否相同: {np.allclose(magnitude1, magnitude2)}")
print(f"模是否为常数: {np.allclose(magnitude1, 1)}")
# 计算相位
phase = np.angle(complex_signal) # 弧度制
phase_degrees = np.degrees(phase) # 角度制
# 计算相位差(相邻采样点之间的相位差)
phase_diff = np.diff(phase)
phase_diff_degrees = np.degrees(phase_diff)
print(f"相位范围: {np.min(phase_degrees):.1f}° 到 {np.max(phase_degrees):.1f}°")
print(f"平均相位差: {np.mean(phase_diff_degrees):.2f}°") // 3
print(f"理论相位差: {360 * freq / sample_rate:.2f}°")
思考问题:
为什么复数信号的模是常数?
两种计算模的方法有什么区别?
相位差与频率和采样率有什么关系?
np.allclose(a,b) 和 a==b 有何差异?
怎么解释平均相位差和理论相位差很不相同(相位缠绕)?
解释 // 3 的意思 φ(t) = 2πf·t
第2部分:Matplotlib基础 (15分钟)¶
基本概念¶
a. 认识图的类型¶
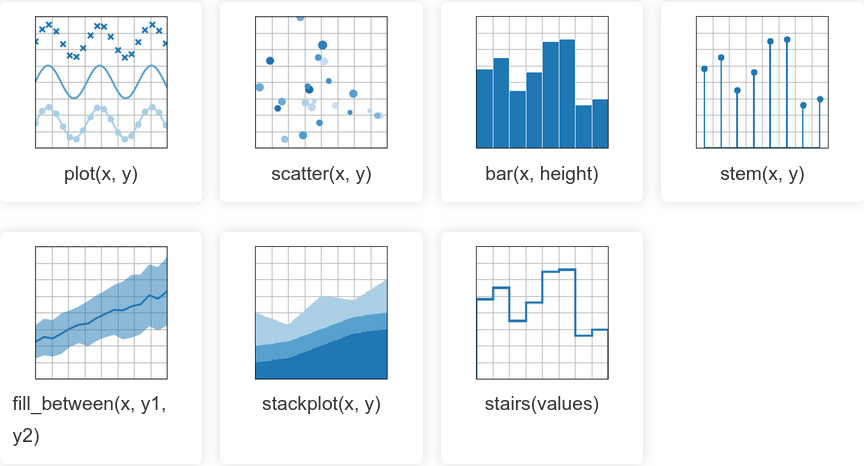
b. 图的部件命名¶
分别说出 figure, title, xlabel, ylabel, grid 是什么?
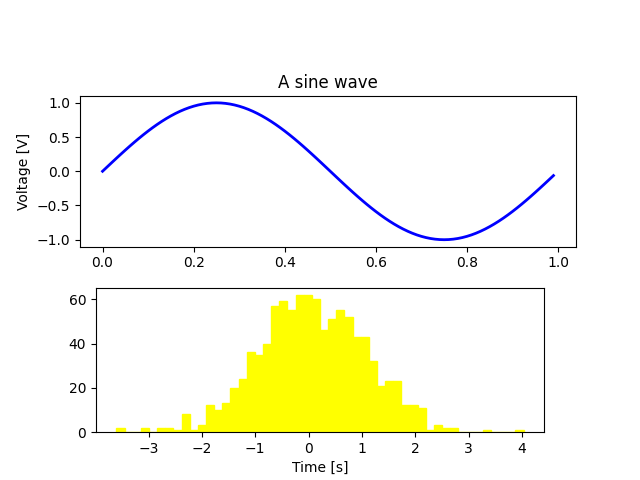
关键概念:
plt.figure()- 创建图形窗口,可设置大小plt.plot(x, y)- 绘制线图,x为横坐标数据,y为纵坐标数据plt.title()- 设置图表标题plt.xlabel()/plt.ylabel()- 设置坐标轴标签plt.grid()- 显示网格线plt.show()- 显示图形
1. 基本绘图¶
先运行程序,把绘图结果与 plt 的各种设置方法对照起来
import matplotlib.pyplot as plt
# 创建时间序列
t = np.linspace(0, 1, 1000) # 1秒时间,1000个采样点
freq = 5 # 5Hz频率
signal = np.sin(2 * np.pi * freq * t)
# 基本绘图
plt.figure(figsize=(6, 4))
plt.plot(t, signal)
plt.title('5Hz正弦波')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.show()
中文会乱码,此时需要通过设置合适的字体解决。也可以将中文标注文字换成英文解决。
[problem 4]:绘制练习2产生的正弦波
# 使用练习2中生成的数据进行绘图
plt.figure(figsize=(12, 8))
# 绘制正弦波
plt.subplot(2, 1, 1)
plt.plot(t, sin_wave, 'b-', linewidth=1.5, label='正弦波')
plt ('1kHz正弦波')
plt ('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
# 绘制余弦波
plt.subplot(2, 1, 2)
plt.plot(t, cos_wave, 'r-', linewidth=1.5, label='余弦波')
plt.title('1kHz余弦波')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
2. 多子图绘制¶
关键概念:
plt.subplot(rows, cols, index)- 创建子图,指定行列和位置plt.tight_layout()- 自动调整子图间距,避免重叠子图编号从左到右,从上到下
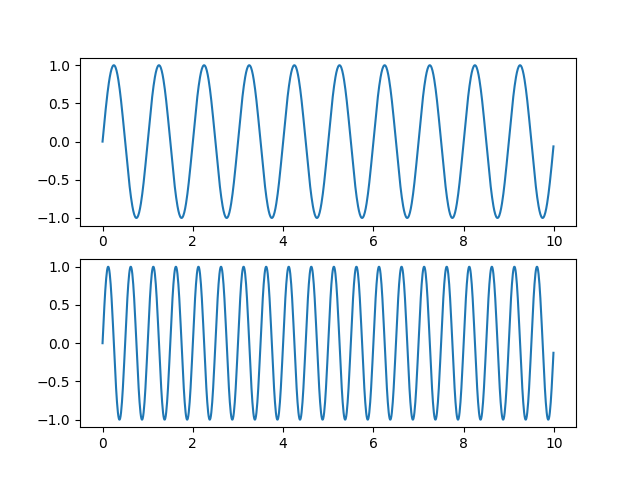
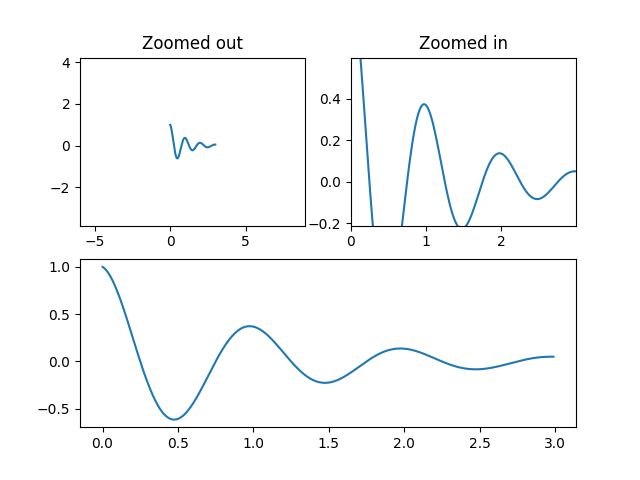
Controlling view limits using margins and sticky_edges — Matplotlib 3.10.7 documentation
# 创建不同频率的正弦波
t = np.linspace(0, 1, 1000)
freq1, freq2 = 2, 10
signal1 = np.sin(2 * np.pi * freq1 * t)
signal2 = np.sin(2 * np.pi * freq2 * t)
# 多子图
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1) # 2行1列的第1个图
plt.plot(t, signal1, 'b-', linewidth=2)
plt.title(f'{freq1}Hz正弦波')
plt.grid(True)
plt.subplot(2, 1, 2) # 2行1列的第2个图
plt.plot(t, signal2, 'r-', linewidth=2)
plt.title(f'{freq2}Hz正弦波')
plt.xlabel('时间 (秒)')
plt.grid(True)
plt.tight_layout() # 自动调整子图间距
plt.show()
[problem 5]:多子图绘制
# 不同子图显示正弦波和余弦波
plt.figure(figsize=(12, 8))
# 子图1:正弦波
plt.subplot(...)
plt.plot(t, sin_wave, '...-', label='正弦波') // blue
plt.title('正弦波 (1kHz)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
# 子图2:余弦波
plt.subplot(...)
plt.plot(t, cos_wave, '...:', label='余弦波') // red
plt.title('余弦波 (1kHz)')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
# 同一子图显示正弦波和余弦波
plt.figure(figsize=(10, 4))
plt.plot(t, sin_wave, 'b-', label='正弦波', linewidth=1) // 将线变粗
plt.plot(t, cos_wave, '...', label='余弦波', linewidth=2) // 用不同的线型
plt.title('正弦波和余弦波比较 (1kHz)')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.show()
3. 绘制实部和虚部¶
关键概念:
复数信号可以用实部和虚部表示
complex_signal.real- 获取实部complex_signal.imag- 获取虚部plt.legend()- 显示图例线型参数:
'-'实线,'--'虚线,':'点线
# 创建复数信号
t = np.linspace(0, 0.1, 500)
complex_wave = np.exp(1j * 2 * np.pi * 10 * t) # 复数指数
plt.figure(figsize=(10, 4))
plt.plot(t, complex_wave.real, label='实部')
plt.plot(t, complex_wave.imag, '--', label='虚部')
plt.title('复数信号的实部和虚部')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.show()
[problem 6]:绘制练习3的复数信号
# 使用练习3中生成的复数信号进行绘图
plt.figure(figsize=(12, 8))
# 绘制实部和虚部
plt.subplot(2, 1, 1)
plt.plot(t, complex_signal.real, 'b-', label='实部 (cos)', linewidth=1.5)
plt.plot(t, complex_signal.imag, 'r--', label='虚部 (sin)', linewidth=1.5)
plt.title('复数信号的实部和虚部 (1kHz)')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
# 绘制模和相位
plt.subplot(2, 1, 2)
plt.plot(t, ..., 'g-', label='模', linewidth=2) //
plt.title('复数信号的模 (1kHz)')
plt.xlabel('时间 (秒)')
plt.ylabel('模值')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
第3部分:综合练习 - 正弦波生成与绘制 (15分钟)¶
简单正弦波生成函数¶
任务描述: 创建一个可重用的正弦波生成和绘制函数库,便于快速生成和可视化不同参数的信号。这些函数封装了NumPy和Matplotlib的核心功能,提供统一的接口来生成和分析正弦波信号。
def generate_sine_wave(freq=1, amplitude=1, duration=1, sample_rate=1000, phase=0):
"""
生成正弦波信号
参数:
freq: 频率 (Hz)
amplitude: 幅度
duration: 持续时间 (秒)
sample_rate: 采样率 (每秒采样点数)
phase: 初始相位 (弧度)
"""
# 生成时间序列
t = np.linspace(0, duration, int(sample_rate * duration)) // 1
# 生成正弦波: A * sin(2πft + φ)
signal = amplitude * np.sin(2 * np.pi * freq * t + phase) // 2
return t, signal
def plot_sine_wave(t, signal, title="正弦波", xlabel='时间 (秒)', ylabel='幅度'):
"""绘制正弦波"""
plt.figure(figsize=(10, 4)) // 3 : 宽10高4
plt.plot(t, signal) // 4
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.grid(True)
plt.show()
[problem 7] :
给
generate_sine_wave()函数增加参数验证: 要求采样率必须大于0,否则程序立即产生值异常; 如果检测到信号频率大于 fs /2,则发出合适的警告信息调用 generate_sine_wave() 产生一段信号,再调用 plot_sine_wave() 绘图
实际应用示例¶
任务描述: 通过实际示例展示正弦波生成函数的应用,包括单个信号绘制、多信号比较和参数变化分析。这些示例演示了如何在实际场景中使用这些函数来解决信号处理问题。
示例1:生成和绘制单个正弦波¶
# 示例1:生成和绘制单个正弦波
print("示例1:单个正弦波")
t, signal = generate_sine_wave(freq=2, amplitude=1.5, duration=2)
plot_sine_wave(t, signal, "2Hz正弦波")
示例2:比较不同频率的正弦波¶
[problem 8] 生成3个不同频率的正弦波,频率分别为: 1,2,5,并在绘图时使用不同的颜色
# 示例2:比较不同频率的正弦波
print("示例2:不同频率比较")
plt.figure(figsize=(12, 8))
# 生成不同频率的信号
frequencies = [1, 2, 5]
colors = ['blue', 'red', 'green']
for i, freq in enumerate(frequencies):
t, signal = generate_sine_wave(freq=freq, duration=1)
plt.subplot(..., 1, i+1)
plt.plot(...) // 1: 使用 colors
plt.title(f'{freq}Hz正弦波')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.grid(True)
plt.tight_layout()
plt.show()
示例3:改变幅度和相位¶
[problem 9] 补全 ... 处的代码,实现改变信号的幅度与相位
# 示例3:改变幅度和相位
print("示例3:幅度和相位变化")
t = np.linspace(0, 2, 1000)
# 不同幅度
signal1 = 1.0 * np.sin(2 * np.pi * 1 * t)
signal2 = ... np.sin(2 * np.pi * 1 * t) //1: 幅度减半
# 不同相位
signal3 = np.sin(2 * np.pi * 1 * t + ...) //2: 相位偏移45度
plt.figure(figsize=(12, 4))
plt.plot(t, signal1, label='幅度=1.0')
plt.plot(t, signal2, '--', label='幅度=0.5')
plt.plot(t, signal3, ':', label='相位偏移45°')
plt.title('不同幅度和相位的正弦波')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.show()
示例4:验证采样定理¶
[problem 10] 对同一个信号使用不同频率采样,观察采样率不足时的影响
import numpy as np
import matplotlib.pyplot as plt
# 建议增加一个更直观的采样定理演示
def demonstrate_sampling_theorem():
"""直观展示采样定理"""
# 高频信号
t_continuous = np.linspace(0, 0.1, 1000)
signal_50hz = np.sin(2 * np.pi * 50 * t_continuous)
# 不同采样率下的重建
sampling_rates = [30, 60, 120] # 欠采样、临界、过采样 [30, 60, 120]
plt.figure(figsize=(15, 10))
for i, fs in enumerate(sampling_rates):
plt.subplot(3, 1, i+1)
# 采样点
t_sampled = np.linspace(0, 0.1, int(fs * 0.1), endpoint=False)
signal_sampled = np.sin(2 * np.pi * 50 * t_sampled)
# 绘制
plt.plot(t_continuous, signal_50hz, 'b-', alpha=0.3, label='original')
plt.plot(t_sampled, signal_sampled, 'ro-', label=f'sampled (fs={fs}Hz)')
plt.title(f'sample rate {fs}Hz - {"undersampling" if fs < 100 else "oversampling"}')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
demonstrate_sampling_theorem()
**练习:**尝试设置不同的 sampling_rates 值,观察采样频率对抽样的影响
建议尝试的采样率:
极低采样: [10, 15, 20] Hz
临界附近: [95, 100, 105] Hz
高采样: [200, 500, 1000] Hz
观察要点:
采样点能否准确表示原始波形?
什么情况下会出现混叠现象?
过采样是否总是更好?
学习要点总结¶
NumPy核心要点:
数组创建:掌握
np.array(),np.arange(),np.linspace()的区别和应用场景向量化运算:理解NumPy的向量化特性,避免使用循环进行数组运算
数学函数:熟练使用
np.sin(),np.cos(),np.exp()等数学函数复数操作:理解复数在信号处理中的重要性,掌握实部、虚部、模和相位的计算
Matplotlib核心要点:
基本绘图:掌握
plt.plot()的基本用法和图表美化多子图:熟练使用
plt.subplot()创建多子图布局图表元素:理解标题、坐标轴、图例、网格等图表元素的设置
信号可视化:能够将NumPy生成的信号数据用Matplotlib直观展示
信号处理概念:
正弦波生成:理解正弦波公式
A * sin(2πft + φ)中各参数的含义采样定理:了解采样率与信号频率的关系,避免混叠现象
正交性:理解相同频率的正弦和余弦信号的平方和为常数
复数表示:掌握用复数表示信号的方法及其优势
实践技能:
函数封装:学会将常用功能封装成可重用的函数
参数化设计:能够通过参数控制生成不同特性的信号
可视化分析:通过图形直观理解信号特性和参数影响
问题解决:能够独立设计实验验证信号处理的基本原理
这个教案专注于基础概念,让你在45分钟内掌握NumPy和Matplotlib的核心功能,为后续的数字信号处理学习打下坚实基础。通过实践练习,你将能够:
快速生成和分析各种信号
可视化信号波形和特性
理解信号处理的基本原理
为更复杂的数字信号处理应用做好准备